Kolmogorov Smirnov Two Sample Test - Definition & Meaning
What is Kolmogorov Smirnov Two Sample Test?
Kolmogorov-Smirnov two-sample test, also known as the K-S test, is used for comparing the cumulative frequency distributions of two samples. It is a non-parametric test i.e. it does not assume fixed structure for a model. It is used for continuous, one dimensional probability distributions. We can use them to test if the two samples have their origin in the same distribution.
Basically they are used to test if there is a considerable difference between two datasets. Graphical presentation of data is possible through the K-S test. Thus, one can detect if the distribution is normal or not. One of its limitations is that it gets sensitive towards the centre of the distribution curve. It is also sensitive to the shape of the distribution.
Formula :Fn(x) = 1/n ∑ Ixi ≤ x
Then K-S statistic is given by
Dn, n’ = sup │F1, n(x) – F2, n’(x)│
Where F1, nand F2, n’– cumulative frequency distribution
The graph below shows how a K-S two sample test distribution looks like.
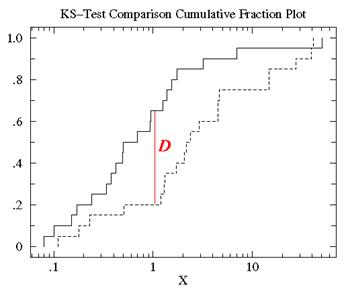
This article has been researched & authored by the Business Concepts Team. It has been reviewed & published by the MBA Skool Team. The content on MBA Skool has been created for educational & academic purpose only.
Browse the definition and meaning of more similar terms. The Management Dictionary covers over 1800 business concepts from 5 categories.
Continue Reading:
