Explained Sum of Square (ESS) - Definition & Meaning
What is Explained Sum of Square (ESS)?
Explained sum of square (ESS) or Regression sum of squares or Model sum of squares is a statistical quantity used in modeling of a process. ESS gives an estimate of how well a model explains the observed data for the process.
It tells how much of the variation between observed data and predicted data is being explained by the model proposed. Mathematically, it is the sum of the squares of the difference between the predicted data and mean data.
Let yi = a + b1x1i + b2x2i + ... + εi is regression model, where:
yi is the i th observation of the response variable
xji is the i th observation of the j th explanatory variable
a and bi are coefficients
i indexes the observations from 1 to n
εi is the i th value of the error term
Then
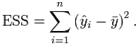
This is usually used for regression models. The variation in the modeled values is contrasted with the variation in the observed data (total sum of squares) and variation in modeling errors (residual sum of squares). The result of this comparison is given by ESS as per the following equation:
ESS = total sum of squares – residual sum of squares
As a generalization, a high ESS value signifies greater amount of variation being explained by the model, hence meaning a better model.
Hence, this concludes the definition of Explained Sum of Square (ESS) along with its overview.
This article has been researched & authored by the Business Concepts Team. It has been reviewed & published by the MBA Skool Team. The content on MBA Skool has been created for educational & academic purpose only.
Browse the definition and meaning of more similar terms. The Management Dictionary covers over 1800 business concepts from 5 categories.
Continue Reading:
