Chi-Square Curve - Definition & Meaning
What is Chi-Square Curve?
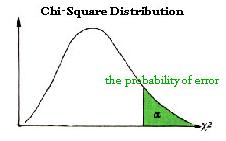
The distribution of the chi-square statistic is called the chi-square distribution. In a statistical experiment of a random sample of size n, having a standard deviation equal to σ, the standard deviation of the sample is equal to s.
A statistic, called chi-square, is defined using the following equation:
Χ^2 = [ ( n - 1 ) * s^2 ] / σ^2
If this experiment is repeated an infinite number of times, a sampling distribution for the chi-square statistic is obtained.
The chi-square distribution has the following properties:
- The mean of the distribution is equal to the number of degrees of freedom: μ = v.
- The variance is equal to two times the number of degrees of freedom: σ^2 = 2 * v
- When the degrees of freedom are greater than or equal to 2, the maximum value for Y occurs when Χ^2 = v - 2.
- As the degrees of freedom increase, the chi-square curve approaches a normal distribution.
This article has been researched & authored by the Business Concepts Team. It has been reviewed & published by the MBA Skool Team. The content on MBA Skool has been created for educational & academic purpose only.
Browse the definition and meaning of more similar terms. The Management Dictionary covers over 1800 business concepts from 5 categories.
Continue Reading:
