Degrees of Freedom
This article covers meaning & overview of Degrees of Freedom from statistical perspective.
What is Degrees of Freedom?
A concept in statistics which is used in estimating statistics of populations from sample of the population. It is commonly abbreviated as df. It can be defined as the mathematical restriction that is in place while calculating an estimate of one statistic from an statistic of another.
Example: The standard normal distribution has a mean of 0 and standard deviation (sd) of 1. The population values of mean and sd are denoted as µ and respectively, and the sample estimates are x-bar and s. In order to estimate , µ must be estimated first. Thus, µ is replaced by X-bar in the formula for sigma. In other words, deviations from µ estimated by the deviations from x-bar. At this point, the restriction that the deviations must sum to zero is applied. Thus, degrees of freedom are n-1 in the equation for s below:
Standard deviation in a population is:
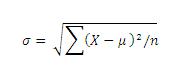
Where is a value from the population, µ is the mean of all , n is the number of in the population, is the summation
The estimate of population standard deviation calculated from a random sample is:
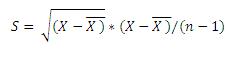
This principle leads to loss of one degree of freedom for each parameter estimated before the standard deviation estimated.
Hence, this concludes the definition of Degrees of Freedom along with its overview.
Browse the definition and meaning of more similar terms. The Management Dictionary covers over 1800 business concepts from 5 categories.
Continue Reading:
