Mesokurtic
This article covers meaning & overview of Mesokurtic from statistical perspective.
What is Mesokurtic?
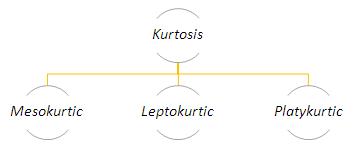
Mesokurtic is the distribution (frequency or graphical) whose kurtosis is similar to the kurtosis of the normally distributed data set. Kurtosis (Greek word meaning bulging) gives the measure of peakedness of a probability distribution of a random variable. It gives the measure of skewness of a distribution and determines how high the distribution is mean centric. Binomial Distributions for which p is nearly equal to ½ are also considered as Mesokurtic.
The peak of any distribution is neither high nor low but is used as reference for other two types of kurtosis-
Leptokurtic – Distribution which has kurtosis greater than a mesokurtic distribution. Tails of such distributions are thick and heavy.
Platykurtic – Distribution which has kurtosis lesser than a mesokurtic distribution. Tails of such distributions are thin and slender.
Kurtosis coefficient defines the peakedness of any distribution. Greater the coefficient, more peaked the distribution around mean is. If the kurtosis coefficient of any distribution is more than 3, it is Leptokurtic and if it is less than 3, it is Platykurtic.
Following graphs are the examples of Mesokurtic, Leptokurtic and Platykurtic distributions:
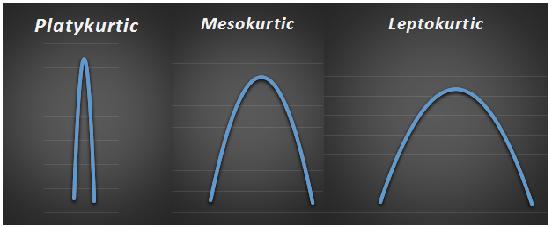
We can see that forms as basis for differentiating Platykurtic and Leptokurtic. It can be observed that Kurtosis of Mesokurtic is more centred towards mean compared to other two distributions.
Hence, this concludes the definition of Mesokurtic along with its overview.
Browse the definition and meaning of more similar terms. The Management Dictionary covers over 1800 business concepts from 5 categories.
Continue Reading:
