Standard Normal Variate (SNV) - Definition & Meaning
What is Standard Normal Variate (SNV)?
A standard normal variate is a normal variate with mean µ=0 and standard deviation σ =1 with a probability density function is
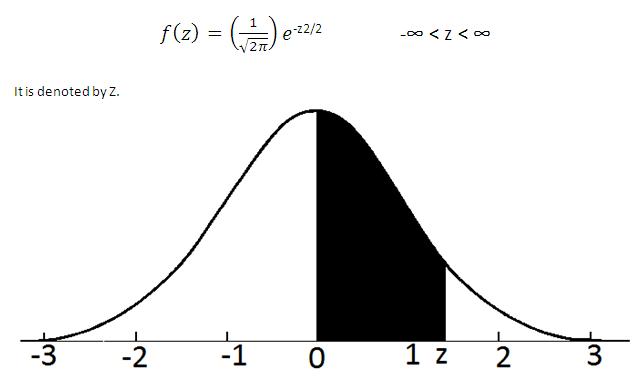
The probability that the variate would take is denoted by the shaded area in the figure.The variate would take a value between 0 and z. This can be read from the table of areas under Standard Normal Curve. The area from 0 to z can be found to any corresponding z from this table. Let X is a normal variate with mean µ and standard deviation σ. Then Z=(X-µ)/σ is a Standard Normal Variate.Hence the Standard Normal Variate can be used to find the probability regarding X.
The expected value of a standard normal variable X is E[X]=0 and the variance is Var[X]=1. The characteristic function of a standard normal random variable X is: ϕX(t) = exp((-1/2)t2).
This article has been researched & authored by the Business Concepts Team. It has been reviewed & published by the MBA Skool Team. The content on MBA Skool has been created for educational & academic purpose only.
Browse the definition and meaning of more similar terms. The Management Dictionary covers over 1800 business concepts from 5 categories.
Continue Reading:
