Simplex Method - Definition & Meaning
What is Simplex Method?
The Simplex Method is a geometric method of solving linear programming problems. The graphical method can be used for problems with two decision variables. But, when we have more than two decision variables and more problem constraints we can use the Simplex method.
It was developed by George B. Dantzig in 1947. It can be understood as an operation on simplical cones. The simplical cones are the corners of a polytope which is defined by the constraints.
ALGORITHM
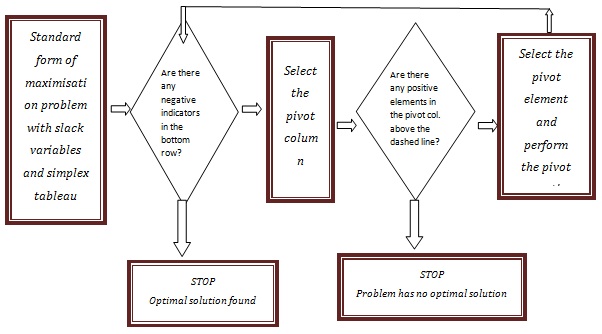
STEPS to solve the problem:
- Convert each inequality constraint to an equality by adding slack variables
- Create initial simplex tableau
- Select the Pivot column
- Select the Pivot row
- Use elementary row operations to calculate new values for pivot row so that the pivot is 1 by dividing every number in the row by pivot number.
- Use elementary row operations to make all numbers in the pivot column equal to 0 except for the pivot number. If all entries in the bottom row are zero or positive, this is the final tableau. If not, go to step 3.
- If you obtain a final tableau, then the problem has a maximum solution given by the lower-right corner of the tableau.
PIVOT terminologies:
- Pivot Column
- Column of the tableau representing the variable to be entered in the solution mix
- Pivot Row
- Row of the tableau representing the variable to be replaced in the solution mix
- Pivot Number
- Element in both the pivot column and pivot row
ADVANTAGES:
- Can be easily programmed and adapted in a software program
- Easier to use than the least-squares method which requires a derivative function
- Efficient than the earlier methods such as Fourier-Motzkin elimination.
- Polynomial time average case complexity
- Given k decision variables, it converges in O(k) operations with O(k) pivots.
DISADVANTAGES:
- It has limited applications
- Not applicable when there are hundreds of decision variables
- It has exponential worst case complexity
- Given k decision variables, it converges in O(2n) operations and pivots in worst-case
Hence, this concludes the definition of Simplex Method along with its overview.
This article has been researched & authored by the Business Concepts Team. It has been reviewed & published by the MBA Skool Team. The content on MBA Skool has been created for educational & academic purpose only.
Browse the definition and meaning of more similar terms. The Management Dictionary covers over 1800 business concepts from 5 categories.
Continue Reading:
